Thuyết tương đối !!!

[cmfc]

Hệ thống quảng cáo SangNhuong.com

Khi nghiên cứu những vật thể chuyển động với vận tốc rất lớn gần bằng với vận tốc ánh sáng, người ta thấy rằng cơ học cổ điển của Newton không còn thích hợp nữa. Do đó cần thiết phải xem lại các khái niệm về không gian và thời gian. Việc xem xét này thực hiện trong thuyết tương đối.

I.PHÉP BIẾN ÐỔI GALILEO (GALILEAN TRANSFORMATION)

1. Hệ qui chiếu- Hệ tọa độ

Muốn xác định vị trí các chất điểm trong không gian thì ta phải biết vị trí tương đối của chúng so với các vật thể làm móc gọi là hệ qui chiếu. Hệ qui chiếu được gắn lên một hệ trục tọa độ.

Ví dụ hệ trục tọa độ DESCARTES 3 trục vuông góc chẳng hạn, khi đó mỗi điểm được đặt trưng bằng tập hợp ba số (x,y,z) ta gọi là các tọa độ của điểm đã cho. Theo thời gian, các điểm có thể dịch chuyển cho nên cần phải bổ sung thêm (tọa độ thời gian) để hình thành khái niệm sự kiện. Sự kiện là một hiện tượng mà nó được xác định bằng 4 tọa độ (x,y,z,t). Ðó là tọa độ của một điểm vũ trụ (một sự kiện) trong không gian 4 chiều. Một tập hợp các sự kiện xảy ra liên tục tạo thành đường vũ trụ.

Hệ qui chiếu gắn lên các vật tự do gọi là các hệ qui chiếu quán tính. Các hệ qui chiếu quán tính có thể chuyển động tương đối với nhau. Khái niệm chuyển động và đứng yên chỉ có tính chất tương đối.

Tính bất biến (Invariant): Khi chuyển từ hệ qui chiếu quán tính S sang hệ qui chiếu quán tính S' hay ngược lại, nếu một đại lượng vật lý nào đó không đổi thì ta gọi đại lượng đó là bất biến (Inv) đối với phép chuyển đổi đó. Nếu một phương trình nào đó là đồng dạng trong phép chuyển đổi ta gọi phương trình đó là phương trình hiệp biến đối với phép chuyển đổi đó.

2. Phép biến đổi Galileo

Xét hai hệ quy chiếu quán tính S và S'. Giả sử hệ S đứng yên, hệ S' chuyển động với vận tốc u so với hệ S. Cho rằng ở thời điểm ban đầu S trùng với S' (Hình 1.1) thì sau thời gian t ta thấy có 1 sự kiện trong hệ quy chiếu S được biểu diễn bằng các toạ độ (x,y,z,t) thì ở hệ toạ độ S' biểu diễn bằng (x',y',z',t')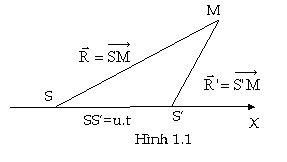

Theo phép cộng vận tốc:

[latex]\vec{SM} = \vec{SS'} + \vec{S'M} \rightarrow \vec{R} = \vec{R'} + \vec{u}.t[/latex]

Giả sử S' chuyển động theo chiều dương của trục Ox đối với S (Hình 1.2), ta có:

x = x' + u.t (1.1a)
y = y' (1.1b)
z = z' (1.1c)
t = t' (1.1d)

Trong biểu thức 1.1d ta hiểu ngầm thời gian trôi như nhau với hệ S và S'.
Đây là bốn công thức cơ bản về phép biến đổi Galileo.
Lấy đạo hàm theo thời gian của các phương trình trên và lưu ý phương trình 1.1d -> dt = dt' ta có công thức cộng vận tốc Galileo:

[latex]v_{x} = v_{x'} + u (1.2a)[/latex]
[latex]v_{y} = v_{y'} (1.2b)[/latex]
[latex]v_{z} = v_{z'} (1.2c)[/latex]

và đối với gia tốc:

[latex]a_{x} = a_{x'} (1.3a)[/latex]
[latex]a_{y} = a_{y'} (1.3b)[/latex]
[latex]a_{z} = a_{z'} (1.3c)[/latex]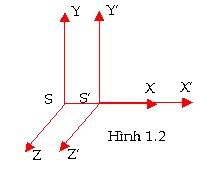

3. Các đại lượng bất biến

Trước hết ta xét tính bất biến của khoảng cách hai điểm (hai chất điểm) j và k bất kì trong phép biến đổi Galileo giữa S và S'. Trong hệ S ta tính độ lớn của véc tơ [latex]\vec{JK}[/latex]:
[latex]\left|\vec{r_{j}}-\vec{r_{k}} \right|= \sqrt{\left(x_{j} - x_{k} \right)^{2} + \left(y_{j} - y_{k} \right)^{2} + \left(z_{j} - z_{k} \right)^{2}} (1.4a)[/latex]
[latex]\left|\vec{r'_{j}} - \vec{r'_{k}} \right|= \sqrt{\left(x'_{j} - x'_{k} \right)^{2} + \left(y'_{j} - y'_{k} \right)^{2} + \left(z'_{j} - z'_{k} \right)^{2}} (1.4b)[/latex]
Thay công thức 1.1 vào 1.4b ta có:
[latex]\left|\vec{r'_{j}} - \vec{r'_{k}} \right|= \sqrt{\left[\left(x_{j} - ut \right) - \left(x_{k} - ut \right)\right]^{2}+\left(y_{j} - y_{k} \right)^{2}+ \left(z_{j}-z_{k} \right)^{2}} [/latex]
[latex] = \left|\vec{r'_{j} - \vec{r'_{k}}} \right|= \sqrt{\left(x_{j} - x_{k} \right)^{2} + \left(y_{j} -y_{k} \right)^{2}+\left(z_{j} - z_{k} \right)^{2}]}[/latex]
[latex]=\left|\vec{r_{j}} - \vec{r_{k}} \right|[/latex] = [latex]\left|\vec{r'_{j}}-\vec{r'_{k}} \right| (1.5)[/latex]
Như vậy khoảng cách hai chất điểm j và k trong phép chuyển đổi Galileo giữa S và S' là bảo toàn. Từ sự bất biến của khoảng cách hai điểm ta suy ra là thể tích của một vật thể là bất biến. Vì khối lượng riêng là hằng số nên khối lượng của vật thể cũng là bất biến trong phép chuyển đổi Galileo giữa S và S'.

Từ các phương trình 1.3 ta thấy gia tốc của một chất điểm là không đổi trong phép chuyển đổi Galileo giữa S và S'

Bây giờ ta xét đến lực tương tác giữa các chất điểm.

Ta biết là lực tương tác giữa các hạt chỉ tùy thuộc vào khoảng cách r giữa chúng vì thế nếu xét lực tương tác F giữa hai hạt ta có thể viết biểu thức tổng quát :
[latex]F = \frac{C}{r^{\alpha}}[/latex]
trong đó C là một hằng số và [latex]\alpha [/latex] > 0

Vậy lực tương tác F giữa hai hạt cũng là bất biến trong phép chuyển đổi Galileo giữa S và S'. Khi xét một hạt riêng biệt, tổng các lực do các hạt khác tác dụng lên nó là chỉ phụ thuộc vào các khoảng cách cho nên hoàn toàn như nhau trong hai hệ S và S'. Vậy lực tổng hợp tác dụng lên một hạt bất kỳ cũng là bất biến trong phép chuyển đổi Galileo giữa S và S' .

Cuối cùng kết hợp khối lượng và gia tốc của một hạt nào đó là không đổi trong phép chuyển đổi Galileo giữa S và S' ta suy ra phương trình Ðịnh luật II Newton là phương trình hiệp biến đối với phép chuyển đổi S và S' tức là bất biến. Chúng ta cũng có thể chứng minh phương trình Ðịnh luật III Newton là phương trình hiệp biến đối với phép chuyển đổi S và S'.

Hãy tiếp tục xét phép biến đổi Galileo trong trường điện từ mà cụ thể là với ánh sáng để xem phép biến đổi Galileo có vận dụng một cách phù hợp không ?

(Còn nữa)
Theo Giáo sư Dương Hiếu Đấu